Exercises: Estimation and confidence intervals
Question 4.1
The data below are taken from the paper: Mothers' dental attendance patterns and their children's dental attendance and dental health, Gratrix et al., 1990, BDJ 168: 441-443). It shows the mean DMFT (total of decayed, missing and filled teeth) of three groups of children along with their standard deviations.
| Children's place of attendance | Number of children | Mean DMFT | Standard deviation of DMFT |
|---|---|---|---|
| General Dental Surgery | 122 | 1·75 | 1·71 |
| Community Dental Surgery | 34 | 1·71 | 1·64 |
| Non-attenders | 21 | 1·52 | 1·72 |
- Calculate the 95% confidence interval for each of the means
- Assuming that DMFT is a normally distributed variable, between what values would we expect 95% of the DMFT values for the 122 children attending the General Dental Surgery to lie?
- Consider your answer to the second part of this question, bearing in mind what DMFT is. What can you deduce about the distribution of DMFT? Is it legitimate or useful to carry out the calculations you did in the first part of the question?
Question 4.2
True or false?
- The 95% confidence interval is wider than the 90% confidence interval.
- We would expect about 95% of a sample to lie within the 95% confidence interval of the sample's mean.
- There is a 95% probability that the true value of the mean lies within the 95% confidence interval.
- A confidence interval is symmetric about the mean.
- The 95% confidence interval is a plausible range of values for the population mean.
- If we repeatedly sampled a population and constructed a 99% confidence interval for the mean of each sample then, in the long run, 99% of the confidence intervals would include the true value of the mean.
If the statement is false explain why.
Question 4.3
How wide would a 100% confidence interval be?
Question 4.4
The data below are taken from the paper: Fluoride release from glass-ionomer and compomer restorative materials: 6 month data (Shaw et al., 1998, Journal of Dentistry 26: 355-359). It shows the amount of fluoride released by three restorative materials (in vitro) after 6 months
| Material | Number of specimens | Mean fluoride release (mg mm-2) | Standard deviation |
|---|---|---|---|
| Ketac-Fil | 5 | 30·62 | 4·85 |
| Chem-Fil Superior | 5 | 12·69 | 2·55 |
| Compoglass | 5 | 10·35 | 1·02 |
Calculate the 95% confidence intervals for each of the means.
What can you infer about how the different materials compare in the light of your results?
Question 4.5
Confidence intervals can be calculated for any summary statistic we derive from a sample. You will commonly see statements such as :
"At 8 years, 25 (11·7%) of the 213 restorations ... had failed"
(A clinical evaluation of posterior composite resin restorations: 8-year findings, Collins et al., 1998, Journal of Dentistry 26: 311-317)
This gives us the percentage of the sample that failed and invites to infer that about 11·7% of the population (of restorations) would fail. It would be more informative if we had a range of plausible values that true mean is likely to lie in, for this we need a confidence interval. The formula for calculating the standard error for a proportion is:
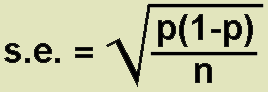
n is the sample size and p is the proportion. (Remember that the proportion is 1/100 of the percentage, in our example we have 11·7% of restorations failing so the proportion of failures is 0·117.)
Adapting our previous definition of a confidence interval for a mean, the 95% confidence interval for a proportioncovers the interval:
'proportion - 1·96 standard errors' to 'proportion + 1·96 standard errors'
Calculate and interpret the 95% confidence interval for the above proportion.
Question 4.6
The data below are taken from the same paper referred to in question 4.5. They show the numbers of three different types of restoration included in the study and how many failed within 8 years. (Each of the materials is given a code letter to make it easier to refer to it in calculations and tables.)
| Material | Code | Number of restorations | Number of failed restorations |
|---|---|---|---|
| Microfilled composite | M | 55 | 9 |
| Fine particle hybrid composite | C | 52 | 8 |
| Relatively coarse particle hybrid composite | P | 54 | 5 |
Calculate the proportion of failures for each material, along with their confidence intervals.
Draw a graph or diagram which presents your results in a suitable manner.
Interpret your results.