Describing Data
Objectives
At the end of the lecture and having completed the exercises students should be able to:
- Choose an appropriate method of graphically displaying a data set
- Choose appropriate measures of location and spread for different data sets
- Calculate some simple summary measures
Bibliography
Altman, D.G., 1991. Practical statistics for medical research, pp.19-38. Chapman and Hall, London.
A good introduction to these concepts. Most other textbooks will be useful here too.
Summary statistics
If we are faced with a large amount of data we may want to describe its more important features more concisely. Two common features we might be interested in are:
- What is the typical (average) value of a variable (what is its location)?
- How much variability is there in the data (how much does it spread out)?
For metric data we might also ask:
- Is the data skewed?
- Is the data bimodal (or multi-modal)?
Measures of Location (Averages)
Mode: The most common value
Median: The middle value
Mean: The sum of all the values divided by the number of cases. (Strictly speaking this is the arithmetic mean.; there are others - geometric mean, harmonic mean - but unless specified mean will mean arithmetic mean.)
Measures of Spread
Range: From the smallest to the largest value. (Can also be expressed as a single number - largest minus smallest - but this isn't as good.)
Interquartile range (IQR): The middle half of the values. i.e. those lying between the first and third quartiles. If we have n observations and we arrange them in order from the lowest to highest (we rank them) then the first quartile (Q1) is the value of the {(n + 1)÷4}th observation. The third quartile(Q3) is the value of the {3x(n + 1)÷4}th observation. If the formulas do not give whole numbers then we have to interpolate. (Note that the second quartile, (or Q2), is simply the median.)
Percentiles: The value below which a given percentage of the cases fall. The value of the kth percentile is obtained by ranking the observations and looking at the value of the {k(n + 1)/100}th observation.
Note that different statistical textbooks will give slightly different ways of calcualting quartiles and percentiles. The difference in the result is slight and usually would have no effect on our interpretation of the statistic.
Standard deviation: A measure of the typical distance from the mean to an observation. The formula is:
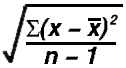
(Or, in words, the square root of the sum of the squared deviations from the mean divided by one less than the number of observations.) To calculate the standard deviation:
- Calculate the mean
- Subtract the mean from the first observation
- Square the result from 2
- Repeat steps 2 and 3 for all the observations
- Add together all the results so far
- Divide by (n - 1) (one less than the number of observations)
- Take the square root of the result from step 6
Or - use a calculator!
Variance: Square of the standard deviation. This is not much used by clinicians writing up their results, it is of more use to statisticians in a mathematical context. You may, however, sometimes find it referred to.
Which measure to use?
Location
| Variable type | Mode | Median | Mean |
|---|---|---|---|
| Nominal | Yes | No | No |
| Ordinal | Yes not recommended |
Yes | No |
| Metric | Yes not recommended at all |
Yes | Yes if data is symmetric and unimodal |
Spread
| Variable type | Range | IQR | Standard deviation |
|---|---|---|---|
| Nominal | No | No | No |
| Ordinal | Yes not usually the best method |
Yes | No |
| Metric | Yes not usually the best method |
Yes | Yes if data is symmetric and unimodal |
Do not use the median together with the standard deviation or the mean with IQR
Note:
Sensitive to outliers: Mean, Standard deviation, Range
Don't make full use of all information: Mode, Median, Range, IQR
Measures of location and skewness
Knowing the values of the mean and median of a distribution can provide some information on the skewness of a distribution.
If the mean is greater than the median then: the distribution is positively skewed; the long tail is on the high (usually right) side of the graph.
If the mean is equal to the median then: the distribution is symmetric.
If the mean is less than the median then: the distribution is negatively skewed; the long tail is on the low (usually left) side of the graph.
Graphs
Use bar charts for categorical data
Pie charts are also used sometimes for categorical data. It is best to avoid these, except, possibly, in the presentation of a single nominal variable for one sample
Metric data
Use histograms or box and whisker plots for metric data
Remember that whilst for bar charts it is the height of the bar that is informative; for a histogram it is the area of the bar that is proportional to the frequency.
A box-and-whisker plot can bring out many useful features of a data set
Remember
When we use a summary statistic to describe a data set we lose a lot of the information contained in the data set.
It is important that we do not use summary measures to obscure vital characteristics of a data set.