Sample size calculations
or
How many patients do we need?
The following is a rough outline to determining how many patients you will need to carry out your study. It is not intended as a substitute for seeking statistical advice but may give you a sense as to whether or not your proposed study is feasible.
1. Determine what is to be the principal outcome measure
Often trickier than statisticians expect it to be! There may be several measures of equal clinical importance. Which measure is most likely to be influenced by the new treatment method? If in doubt, it is usually better to calculate required patient numbers on the basis of each important measure, rather than trying to combine all into a single complex scale.
2. Judge a realistic true underlying difference between the treatments
Possibly the most annoying question a statistician will ask, which invariably gets a response along the lines of "If I knew what the difference was going to be, I wouldn't need to do a trial!". What we mean is, "How much difference would there really have to be between the treatments to make it worth your while concluding that there is a difference?". For example, if the current treatment has an 80% success rate, is it worth knowing that a new treatment has an 81% success rate? This will depend on all sorts of things: gravity of outcome; side effects; relative convenience to patients and staff; and, increasingly, relative costs. How big a difference would persuade you to change your routine clinical practice?
3. Select (arbitrary) statistical power and significance levels
Even if there is a 'true underlying difference' between treatments, you may be unlucky and miss it. The more patients you study, the higher the chance you won't miss it. This chance is the statistical power of the study. Significance level is conventionally set at 5% (α=0·05). Similarly, although not so universally, power is often set to be 80%, sometimes 90%, and rarely 95%. The reasons why such low power is accepted are hazy, but appear to have more to do with pragmatism than logic.
4. Use appropriate formula for chosen outcome measure
The two most common formulae are given below with examples. Almost all studies can be twisted to fit one or other. Given the mystic hand-waving approach to guessing realistic treatment differences, subtleties of formula choice for the vast array of potential designs seems futile. However, a good book including far more in the way of formulae and nomograms is available in the medical library: Machin & Campbell. Statistical Tables for the Design of Clinical Trials.
5. Wonder why required number of patients is so high!
If the numbers aren't much higher than anticipated, either your anticipation was pessimistic, your estimate of differences optimistic, or you've made a mistake in the calculations! The sad truth is that the vast majority of research is hopelessly under-powered. Only with huge advances in care can small single centre studies establish the benefits. If the calculated numbers are too high, therefore, should this work be considered as pilot data to determine whether there is sufficient promise in the new treatment to justify major funding; or can collaborators be found locally or nationally?
Calculations for trials with patients in two groups
1. Comparing proportion of 'successes'
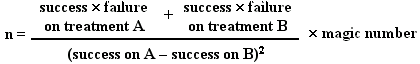
2. Comparing means of normally distributed outcome
![]()
n is the number of patients per group
What if there are no pilot data, preliminary reports or previous literature on which to base your estimate of the standard deviation?
One rule of thumb is that the standard deviation will be about one quarter of the range of usual measurements. For example, if the mean on current treatment is about 80, and you'd anticipate 95% of people to score between 60 and 100 (range=40), then the standard deviation is about 10.
Magic Number
This value is determined by the required power and significance level. For common values it is tabulated below:
| Statistical Power | ||||||||
| 50% | 60% | 70% | 80% | 90% | 95% | 99% | ||
| Significance Level | 5% | 3·8 | 4·9 | 6·2 | 7·8 | 10·5 | 13·0 | 18·4 |
| 1% | 6·6 | 8·0 | 9·6 | 11·7 | 14·9 | 17·8 | 24·0 | |
Example
Consider a trial looking for improvement from 85% success rate on the current treatment (A) to 90% on a new treatment (B), and requiring an 80% chance of detecting a difference at the 5% significance level (α=0·05).
From first formula and table,
![]()
NOTE that this is 680 patients per treatment or 1360 in total.