Estimation and confidence intervals
Objectives
At the end of the lecture and having completed the exercises students should be able to:
- Describe the characteristics of the normal distribution in statistical terms previously encountered
- Explain the concept of a confidence interval and how it relates to an estimated parameter
Bibliography
Gardner, M.J. & D.G. Altman, 1989. Statistics with confidence. The Universities Press, Belfast.
This gives a very thorough introduction to the calculation and use of confidence intervals for those who wish to read further.
Altman, D.G., 1991. Practical Statistics for Medical Research. Chapman & Hall, London. pp. 51-59; 133-143.
These two passages provide more information on the normal distribution and how to test distributions for normality.
The normal distribution
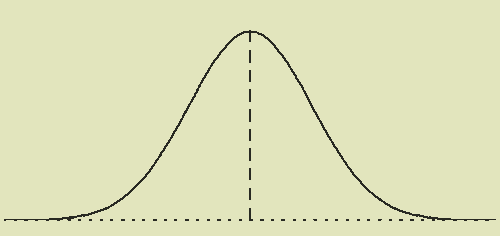
The normal distribution
Sometimes called a Gaussian distribution
Key features
- Symmetric
- Not skewed
- Unimodal
- Described by two parameters
Parameters of normal distribution
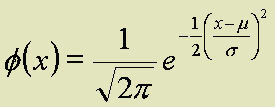
The equation of the normal distribution. Do not memorise this!
Explanation of equation
- μ and σ are parameters
- μ is the mean
- σ is the standard deviation
- e and π are constants
z-scores
To transform data from a normally distributed data set to a z-score (standard normal deviate, normal score):
- Subtract the mean
- Divide by the standard deviation
Transforms data to a normal distribution with μ = 0 and σ = 1. This particular normal distribution is known as the standard normal distribution.
The standard normal distribution
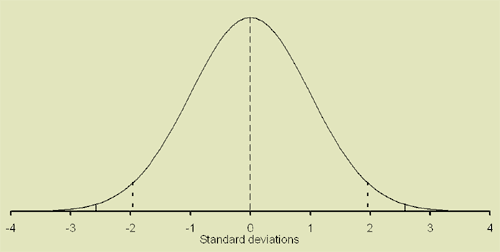
The standard normal distribution
The interval
'population mean - 1·96 standard deviations' to 'population mean + 1·96 standard deviations'
Contains 95% of the population
The interval
'population mean - 2·58 standard deviations' to 'population mean + 2·58 standard deviations'
Contains 99% of the population
Why do we use the normal distribution?
- Many biological variables follow a normal distribution
- The normal distribution is well-understood, mathematically
Estimation
What factors will make our estimate of a mean better?
- A large sample size
- A homogenous population (small standard deviation
When we have taken a sample we want to use it to get information about the population from which it is drawn e.g. we want to know the population mean so we take a sample. The sample mean is taken as our best guess at the population mean. The same applies to other parameters - parameters here can mean a feature of a population we are interested in.
We also want to know: how good is the guess?
NB: use Latin letters for sample estimates and Greek letters for population parameters.
Standard error
Standard error is a measure of how good our best guess is.
We have a simple formula to give us the standard error:
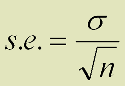
standard error = (standard deviation)/(square root of number of observations)
i.e. the bigger the sample, the smaller the standard error
If we repeat the sampling and estimation process many times we get a distribution of estimates.
For a normal population the distribution of estimates of the mean is itself a normal distribution with a standard deviation equal to the standard error.
The standard error is always smaller than the standard deviation
The distribution of sample means will be nearly normal whatever the underlying distribution (the central limit theorem) if the sample sizes are large.
Confidence intervals
The interval:
'sample mean - 1·96 standard errors' to 'sample mean + 1·96 standard errors'
is the 95% confidence interval.
(Using 2·58 instead of 1·96 will give us the 99% confidence interval)
If we take a sample from a population and calculate the mean of that sample and its associated 95% confidence intervals, there is a 95% probability that the confidence interval will include the true mean of the population
A confidence interval gives us a plausible range of values for an estimate, usually on a clinically useful scale.
Confidence intervals can be calculated for other quantities e.g. medians, proportions (see Gardner & Altman)
Example
Number of teeth of nine patients attending a clinic:
32, 32, 31, 30, 28, 28, 27, 25, 18
Mean = 27·9
Standard deviation = 4·4
What is the confidence interval of the mean?
The number of patients is 9. We can use the formula to calculate the standard error:
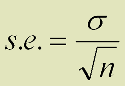
This becomes:
s.e. = 4·4/3 = 1·467
The 95% confidence interval for the mean is:
'sample mean - 1·96 standard errors' to 'sample mean + 1·96 standard errors'
or:
27·9 - 1·96x1·467 to 27·9 + 1·96x1·467
So, the 95% confidence interval of the mean is:
From 25·0 to 30·8
Note that we do not write 25·0 - 30·8, because the hyphen can become confused with a minus sign in some circumstances always use From ... to .... Also note that the answer was rounded to the appropriate number of decimal places at the final step and not before. This is necessary to avoid errors creeping in.